河图、洛书是中国古代流传下来的两幅神秘图案，蕴含了深奥的宇宙星象之理，被誉为“宇宙魔方”。从数学角度来讲，洛书是世界上最古老的三阶幻方，它有3行3列，而且3横行的3个数之和、3竖列的3个数之和、两对角线的3个数之和都等于15。类似地，可以用1到16排成一个四阶幻方，使每条线上加起来都是34。让我们一起来感受洛书的智慧与幻方的神奇吧！

　　什么是幻方

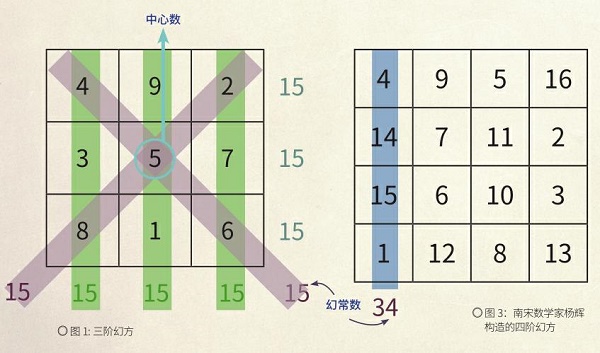
　　幻方是把从1到n2的自然数排成的行列的正方形数表，其每行、每列、每条对角线上的数之和都相等，这个“和”称为幻常数，幻常数等于 。图1是一个三阶幻方，即n等于3，n2等于9，幻常数等于15。已知三阶幻方有8组，四阶幻方有880组(1693年数据)，五阶幻方有275305224组(1973年数据)，更高阶幻方的组数至今还无法确定。

　　洛书的传说与纵横图

　　世界上最早的幻方出现在中国。相传，上古时期，洛河中浮出神龟，背驮洛书，献给大禹。大禹因此治水成功，划天下为九州，制定九章大法，治理国家。在长期的历史发展中，洛书演化为中国文化的代表符号之一，并被赋予多种解释。1977年，阜阳西汉汝阴侯墓（位于安徽省阜阳市）出土的太乙九宫占盘，为洛书提供了考古实物证据。

　　图2是洛书的示意图。在数学上，洛书刚好是三阶幻方，按现代书写顺序，正是图1。

　　幻方在中国古代被称为“纵横图”。南宋数学家杨辉的著作《续古摘奇算法》中记录了从三阶直到九阶幻方，连同十阶的半幻方(不满足对角线条件)，分别称为四四图、五五图、六六图、衍数图、易数图、九九图、百子图，还给出了三阶、四阶幻方构造方法的说明。杨辉还研究了幻方的6种变形。图3是杨辉构造的四阶幻方。

　　幻方在现代科学技术中也有广泛的应用，例如：它的构造原理与飞机的电子回路设置密切相关，研究人员创造的64阶方阵仪可以用于计算机、测量仪、通信交换机及水电、火电、航空等的管理系统。

图2：洛书示意图


南宋数学家杨辉的著作《续古摘奇算法》

　　一般三阶幻方的规律

　　作为推广，一般允许构成幻方的数字为任意实数，也不要求这些数不同。完成一般三阶幻方填充，常常变身为小学奥数练习题目。其实，如果知道规律，解答这类题目易如反掌。

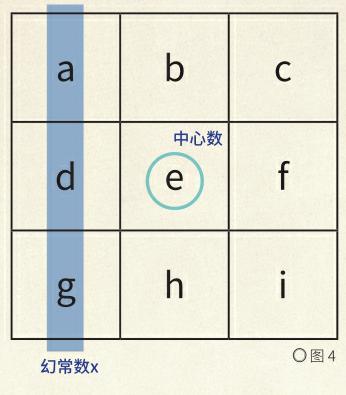
　　规律1：一般三阶幻方的幻常数等于中心数的3倍。即如图4所示，设一般三阶幻方的9个数字分别为a,b,c,d,e,f,g,h,i,幻常数为x，e就是中心数，3e=x 。

　　规律2：一般三阶幻方的一个角顶数的二倍等于紧邻对角顶的两数之和。即2a=f+h，2c=d+h，2g=b+f，2i=b+d。

知识拓展 幻方的传播与文化影响

　　幻方的思想从中国传播到日本、朝鲜、印度、泰国，后又陆续传至阿拉伯世界、欧洲和美洲，受到世界各地人们的喜爱，常被做成平安符、幸运符等装饰物。

　　金庸的武侠小说《射雕英雄传》设置了黄蓉在桃花岛回答幻方问题的情节：

　　黄蓉笑道：“不但九宫，即使四四图，五五图，以至百子图，亦不足为奇。就说四四图罢，以十六字依次作四行排列，先以四角对换，一换十六，四换十三，后以内四角对换，六换十一，七换十。这般横直上下斜角相加，皆是三十四。”

　　黄蓉的这段话说的正是前文所述杨辉的三阶幻方作法和四阶幻方作法(图3)。

2014年，中华人民共和国澳门特别行政区发行的幻方邮票第一组6张，其中展示了特殊的幻方、构造方法、变种等多方面内容（图片来源/维基百科）




文艺复兴时期德国画家丢勒(Albrecht Dürer)1514年创作的著名铜版画《忧郁I》。画面右上角是一个四阶幻方，底行中间的两个数字暗示了创作年份（图片来源/维基百科）

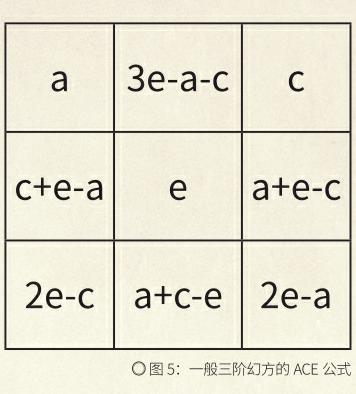
　　规律3：一般三阶幻方由某3个位置的数完全决定。比如，任意确定的a，c，e值，就能完成三阶幻方的填充，而且填充方式只有一种(如图5)。我们把这组填充公式称为一般三阶幻方的ACE公式。

　　读者可以尝试自己找出一般四阶幻方的公式，这是解一个16元一次方程组的问题。

　　新想法——面积三阶幻方

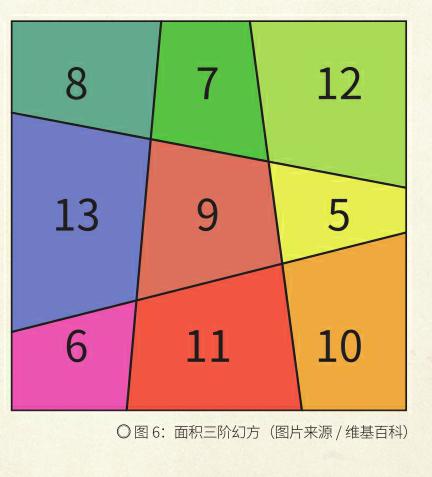
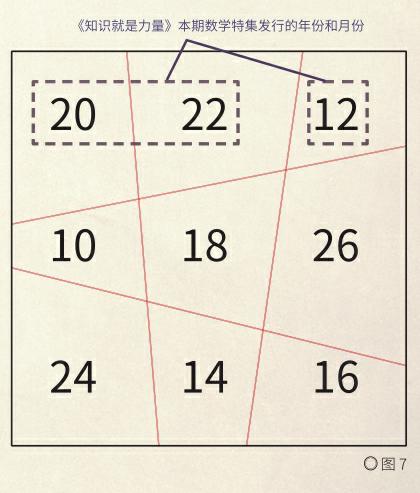
　　幻方研究专家将一般三级幻方“更新升级”，用两条横斜直线和两条竖斜直线，把正方形分成9个四边形，就得到面积三阶幻方，如图6。类似的有面积四阶幻方。这是幻方研究的新想法。

　　笔者特别设计了一个面积三阶幻方(见图7)，第一行的面积数值刚好是《知识就是力量》本期数学特集发行的年份和月份。

　　在文章的最后，笔者留给读者们一个挑战问题：用互不相同的平方数构造一个三阶幻方。这是从瑞士大数学家欧拉(L.Euler,1707—1783年) 开始，至今仍未解决的问题。也许本文的读者里面就有将来解决这个难题的人！

　　（责任编辑 / 高琳 美术编辑 / 周游）

扫二维码参与互动，有机会获得《知识就是力量》精美礼品